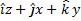
1. Calculate  the flux  of the field over  the surface of a right circular cylinder of radius R and height h in the first octant, i.e. in the region (x>0, y>0, z>0).

For the curved surface of the cylinder, the unit vector is which gives  Parameterize ,Since we are confined to the first octant The flux through the slant surface is .  The top and the bottom caps are in the  directions, the contribution from these two give zero by symmetry.  There are two more surfaces if we consider the first octant, they are the positive x-z plane and the positive y-z plane., the normal to the former being in the direction of  while that for the latter is along  directions. The flux from the former is , while that from the latter is .  Adding up all the contributions, the total flux from the closed surface is zero. This is consistent with the fact that the divergence of the field is zero.

2. Evaluate the surface integral of the vector field 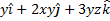over the surface of a unit cube with the origin being at one of the corners.

There are six faces. For the face at x=0, since the surface is directed along  direction, the surface integral is   The face at x=1 gives +1/2. The faces at y=0 and that at z=0 gives zero because the field is proportional to y and z respectively. The contribution to flux from y=1 is 1 and that from z=1 is 3/2. Adding, the flux is 5/2 units.  This can also be done by the divergence theorem. Divergence of the field is  2x+3y, so that the volume integral is

3. Calculate  the flux of 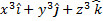over the surface of a sphere of radius R with its centre at the origin.

The divergence of the given vector field is . Thus, by divergence theorem, the flux is  . We can show this result by direct integration. The unit normal on the surface of the sphere is given by  , so that the flux is  This integral can be conveniently evaluated in a spherical polar coordinates with  The surface element on the sphere is  . By symmetry, the flux can be seen to be  . (Note that we decided to do the integral involving z4 rather than x4 or y4 because the azimuthal integral gives 2p in this case.  The integral is easy to perform with the substitution  , which gives the flux to be  .

4.Calculate the flux of through the surface defined by a  cone and the plane  

The divergence of the field is 3. The flux, therefore, is  3 times the volume of the cone which is The flux is thus  The  direct calculation of the flux involves two surfaces, the slant surface and the cap, as shown in the figure. The cap is in the xy plane and has an outward normal . The flux (because on the cap z=1 and the cap is a disk of unit radius).  Thus it remains to be shown that the flux from the slanted surface vanishes. At any height z, the section parallel to the cap is a circle of radius z. Since, the height and the radius of the cap are 1 each, the semi angle of the cone is 45⁰.

Thus the normal to the slanted surface has a component  along the z direction and  in the x-y plane. The component in the xy plane can be parameterized by the azimuthal angle  and we can write  . The area element can be written as  , the factor  appears because the length element is along the slant. Thus the contribution from the slanted surface is  . Using  , this integral can be evaluated and shown to be zero.

5. Evaluate the flux through an open cone with  for the field .

This problem is to be attempted similar to the problem  5 of the tutorial, i.e., by closing the cap and subtracting the contribution due to the cap. The divergence being 3, the  flux from the closed cone is 3 times the volume of the cone which gives 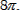  The contribution from the top face (which is a disk of  radius 2 ) is 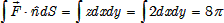. Thus the net flux is zero.  (You can also try to get this result directly as done in problem 4, where we showed that the flux from the curved surface is zero).